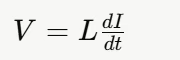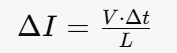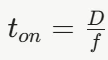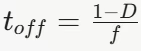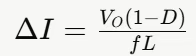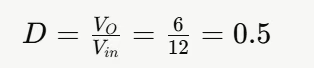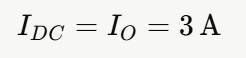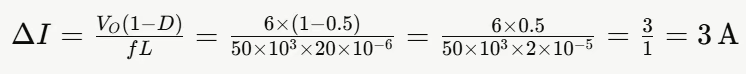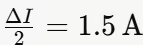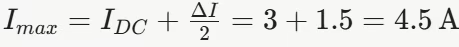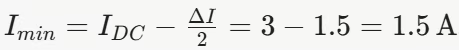BUCK 降压电路是一种常见且重要的电路类型，其功能是将较高的输入电压转换为较低的输出电压，以满足不同电子设备的用电需求。在这个电路中，电感是一个关键元件，它承担着储存和释放能量的重要任务。电感的电流由平均直流分量和交流纹波 ΔI 两部分组成。深入理解这两部分电流的构成和计算方法，对于准确理解和优化 BUCK 电路的设计至关重要。

电感电流构成

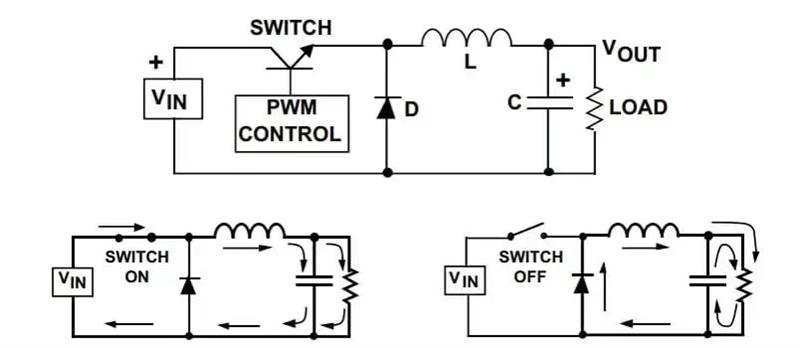
BUCK 电路主要由开关 MOSFET、二极管、电感和电容等元件组成。其工作过程可以分为两个阶段：

• 开关导通阶段：当开关 MOSFET 导通时，输入电压通过电感向负载供电。在这个过程中，电感会储存能量，电感中的电流会逐渐增加。
• 开关关断阶段：当开关 MOSFET 关断时，电感会通过二极管向负载释放之前储存的能量，此时电感中的电流会逐渐减小。

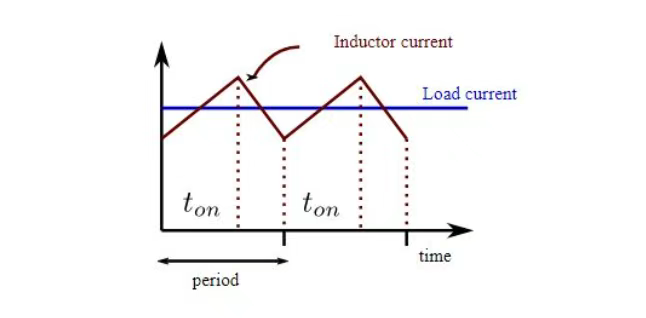
这种周期性的开关行为使得电感电流呈现出锯齿状的波形，其中包含了稳定的直流分量和上下波动的交流纹波。

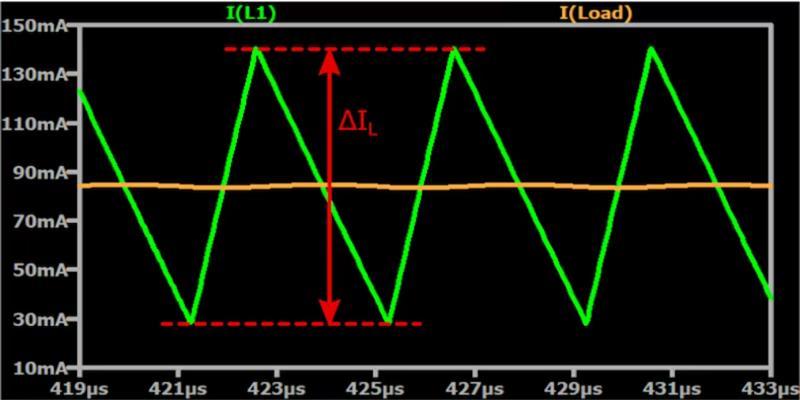
电感电流主要可以分为以下两部分：

1. 平均直流分量 IDC：这是电感电流在一个开关周期内的平均值。在连续导通模式下，它通常等于负载的输出电流 Io。这意味着在稳定的工作状态下，电感向负载传递的平均电流与负载所需的电流是相等的。
2. 交流纹波△I：这是电感电流在直流分量上下波动的峰峰值，它是由开关过程中的充放电引起的。交流纹波的大小反映了电感电流在一个开关周期内的变化幅度。

电感电流计算

接下来，我们将分别介绍这两部分电流的计算方法，这里的计算是针对连续导通模式 CCM 进行的。

1. 计算平均直流分量 IDC：在连续导通模式 CCM 下，电感电流始终大于零。由于在稳态运行时，电感通过周期性的充放电将能量传递给负载，而电容的平均电流为零，所以电感电流的平均值等于输出电流 Io，即 IDC = Io。例如，如果负载电流为 2A，那么电感电流的平均值 IDC 也为 2A。需要注意的是，电感的平均直流分量 IDC 与占空比 D 没有直接关系，它仅仅由输出电流决定。
2. 计算交流纹波△I：交流纹波△I 是电感电流在开关周期内的峰峰值，它反映了电流的变化量。其计算基于以下公式：

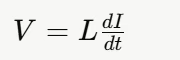
将上述公式改写为离散形式可得：

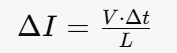
其中，V 是电感两端的电压，△t 是电压作用的时间，L 是电感值。

在 BUCK 电路中，电感电压会随着开关状态的变化而变化：

• 导通时：电感电压为 Vin－Vo，持续时间为

• 关断时：电感电压为－Vo，持续时间为

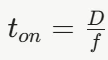
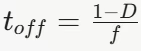
其中，Vin 是输入电压，Vo 是输出电压，D 是占空比（在理想情况下 D = Vo / Vin），f 是开关频率。

在稳态下，导通时的电流增量等于关断时的电流减量。因此，纹波可以通过以下公式计算：

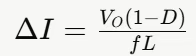
从这个公式可以看出，电感纹波电流的大小与输出电压 Vo、占空比 D、开关频率 f 和电感值 L 相关，而与平均电流 Io 无关。

计算实例

为了更直观地理解上述计算方法，我们假设一个 BUCK 电路的参数如下：

• 输入电压 Vin = 12V
• 输出电压 Vo = 6V
• 电感值 L = 20μH
• 开关频率 f = 50kHz
• 输出电流 Io = 3A

1. 计算占空比 D
   

   

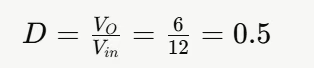
2. 计算直流分量 IDC
   

   

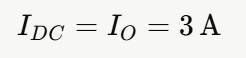
3. 计算交流纹波△I
   

   

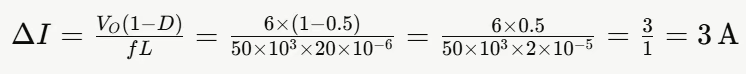
4. 确定电流范围
   电感电流在 IDc 上下波动，波动幅度为：
   

   

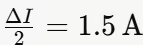
值为：

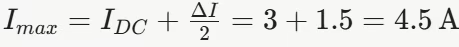
值为：

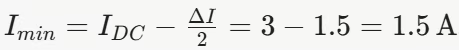
因此，在这个例子中，电感电流在 1.5A 至 4.5A 之间波动，平均值为 3A。

需要注意的是，以上分析是假设电路工作在连续导通模式 CCM 下，即电感电流始终大于零。如果负载电流 Io 较小，电感电流可能会降至零，此时电路将进入不连续导通模式 DCM。在不连续导通模式 DCM 下，纹波的计算需要考虑电流为零的时段，其计算公式会更加复杂。