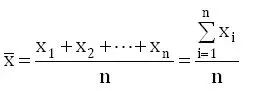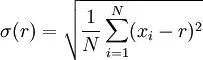在半导体制造的复杂流程中，常常会面临将一个机台扩展到另一个机台，或者需要评价两组数据是否符合生产要求的情况。此时，利用质量工具进行科学判定新的机台能否进入产线生产就显得尤为重要。而在这其中，MR（Match Rule，匹配规则）发挥着关键作用。

MR 的基本概念与判定标准

MR 作为一种重要的质量判定工具，有不同的类型，如 M.R - 1 和 M.R - 2，它们各自有着明确的判定标准。

• M.R - 1：当 M.R - 1 ≤ 1 时，表示两组数据无明显差异；当 M.R - 1 > 1.0 时，则表明两组数据有显著差异。
• M.R - 2：若 M.R - 2 ≤ 1.5，说明数据之间无明显差异；当 M.R - 2 > 1.5 时，意味着数据有显著差异。

MR 的计算公式

• M.R - 1 公式：M.R - 1 = |New.AVG - BSL.AVG| / σ.BSL 。其中，New.AVG 代表新数据的平均值，BSL.AVG 代表原本数据的平均值，σ.BSL 代表原本数据的标准差。这个公式通过比较新数据和原本数据的平均值差异，并结合原本数据的标准差，来衡量两组数据的差异程度。
• M.R - 2 公式：M.R - 2 = σ1 / σ2 ，它代表着数据 1 与数据 2 两者之间的离散程度。当 M.R - 2 ≤ 1.5 时，表明扩展的机台对应的数据与 BSL（baseline）机台对应的数据（如 THK、CD）离散程度一致，这样的机台扩展是可以被接受的，能够放心地用于生产。这对于保证生产的稳定性和产品质量的一致性具有重要意义。

MR 计算中涉及的主要数据

平均值

平均值即算术平均值，它是一组数据的总和除以数据的个数。其计算方法在数学和统计学中是基础且重要的，在半导体数据处理中，平均值能够反映一组数据的总体水平。例如，在评估机台生产的产品某一参数时，平均值可以让我们对产品的整体情况有一个初步的了解。

标准差

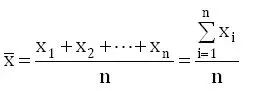
标准差是样本中各个个体与其平均数的差的平方的算术平均值的平方根，它反映的是一个数据集的离散程度。标准差的值越大，说明数据越离散，即个体间差距越大。在半导体制造中，标准差能够帮助我们了解机台生产的产品参数的稳定性。如果标准差较大，说明机台生产的产品在该参数上波动较大，可能需要对机台进行调整或维护。

MR 在半导体制造中的重要性

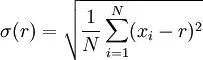
在半导体制造过程中，机台的性能和数据的稳定性直接影响着产品的质量和生产效率。通过 MR 的计算和判定，我们可以科学地评估新的机台是否适合进入产线生产，避免因机台性能差异导致的产品质量问题。同时，对于已经在产线中的机台，定期进行 MR 分析也可以及时发现机台性能的变化，以便采取相应的措施进行调整和优化。