金属导电电子之间的相互作用

出处：老太阳集团tcy8722网站电子市场网发布于：2024-12-16 16:04:50

　　在本教程中，我们将学习 Hartree 算法。这是一个非分析封闭程序，通过连续近似的迭代过程，我们可以在考虑相互库仑相互作用的情况下确定固体中电子的量子力学状态。在第 0 个近似值中选择合适的波函数保证了算法的收敛性。
　　介绍
　　前几期取得的结果基于 Bloch 定理1，它使用 Born-Oppenheimer 近似的零步长作为起点2.我们记得，这个定理是晶格平移离散对称性的结果，其中电子被认为是独立的和非相互作用的。更明确地说，我们注意到：

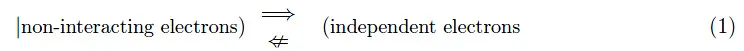
　　我们所说的“独立电子”是指：电子系统的哈密顿量是单个电子的哈密顿量之和。这样，与电子系统相关的希尔伯特空间是与单个电子相关的希尔伯特空间的直接乘积。方程（1）意味着电子的独立性是它们不相互作用的必要但不是充分条件。我们之所以坚持这一方面，是因为它在所提出的方法中起着基础性的作用。考虑非独立电子系统会导致施罗定谔类型的微分方程，该微分方程甚至不能进行数值积分。
　　B-O 步骤 0 中的问题设置

　　Hartree 算法是数学家 D.R. Hartree 于 1928 年提出的一种计算过程，称为自相容（或自洽）场法3，在与 Niels Bohr 进行了一系列对话之后。这种计算方案在原子物理学中用于多电子原子的研究，并且可以扩展到固态物理学，特别是金属。这是一种使用 Born-Oppenheimer （B-O）近似值作为起点的蛮力攻击程序。具体来说，在 B-O 的第 0 步，我们假设正离子在 Bravais 晶格的晶格位置是静止的：

　　电力电子学科学笔记：金属导电电子之间的相互作用
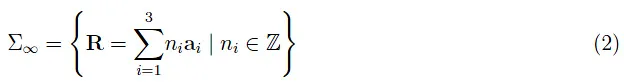
　　其中三元组 {a我} 定义晶格的基本向量系统。如果 Z 是单个原子的原子序数，则核电荷为 +Ze，其中 e > 0 是电子电荷的。为了更定量，我们用 0 < z ≤ Z 表示单个原子的电离度。简单来说，每个原子都失去了 z 电子。

　　在方程（2）中，晶格具有无限延伸，下标的含义和晶格位点中离子分布的周期性从该延伸开始。我们记得，这种无限延伸可以通过 Born-Von Karman （BVK）条件人工再现。在元件中：

　　电力电子学科学笔记：金属导电电子之间的相互作用
　　其中 σα 是一个 BVK 域，即有限扩展的单个域，然后无限复制。忽略电子之间的相互作用，晶格（3）表现出离散的平移对称性，如前所述，这导致了布洛赫定理。因此，我们有一个独立电子的特例，每个布洛赫波都是多电子原子中原子轨道的模拟。因此，每个 Bloch 特征函数的晶体轨道的名称。在电子之间添加库仑相互作用意味着打破离散平移对称性，因此使布洛赫定理无效。换句话说，布洛赫波是单电子态的近似值。
　　任意取体积 V 的 BVK 域，我们用 N 表示（离子）离子的总数。由此可见，电子系统由 N 构成（EL） = N（离子）z 电子。B-O 的第 0 步告诉我们，假设离子是静止的，我们必须参考电子系统。因此，我们有一个由 N 构成的非相对论量子系统（EL）粒子;我们忽略了自旋-轨道相互作用，因为电子的本征磁矩（即由于电子自旋）与轨道运动产生的磁场之间存在相互作用的势能。
　　观察：自旋-轨道相互作用的解析处理需要 Dirac 方程。
　　我们仍然可以考虑自旋自由度，将波函数乘以适当的双分量旋量。无论如何，电子自旋在 Pauli 排除原理中起着重要作用。从自旋中抽象出来，即只考虑轨道自由度，我们写出在适当的希尔伯特空间中定义的哈密顿算子。

　　与非相对论量子力学的所有问题一样，我们然后为上述算子求解相应的特征值方程，即确定能量的特征函数和特征值。通用特征函数只不过是电子系统的集体量子态，而能量 E 的特征值是电子的总能量。因此，我们有一个与时间无关的 N 组薛定谔方程（EL）电子：

　　正如我们在参考资料中所展示的那样4.
　　Hartree 算法
　　偏微分方程（4）甚至不能用数值求解。然后，Hartree 使用了独立电子近似，它允许电子系统的哈密顿量表示为单电子哈密顿算子的总和。这相当于将与电子系统相关的希尔伯特空间“碎裂”为 N （el）希尔伯特空间的张量积，每个空间都与一个电子相关联。反过来，单个电子在离子和剩余 N 产生的电场中移动（EL）? 1 个电子。
　　产生的势能表示为两个贡献的总和，一个是由于正离子，另一个是由于剩余的电子。项很容易计算，因为离子在晶格位点中是静止的。结果是空间坐标中的周期函数，其周期等于单个晶格步长一个我 = |a我|对于 i = 1， 2， 3。如果我们只考虑这项，哈密顿量将具有 step 的翻译的对称性一个我，因此根据 Bloch 定理，我们将得到通常的调幅平面波。
　　正是第二项，即由于与剩余电子相互作用而产生的项，破坏了这种对称性。此外，它更难计算。为此，使用了静电学中众所周知的概念，其中包括首先确定剩余电子产生的电场的电位，其计算需要了解 N 系统的电荷密度（EL） 1 个电子。后者表示为单个电子的电荷密度之和。
　　一个合理的方法是假设一个以电子所在点为中心的狄拉克 delta，我们想要表示其电荷密度。但 Hartree 更聪明，因为与波力学一致，他假设电子电荷的单电子波函数的平方模为电荷密度，然后对所有 N 求和（EL） 1 个电子。
　　在这里，对于波函数，我们准确地考虑了我们正在寻找的特征函数。经过多次操作，我们得出了一个未知函数 ψj （r）中的 N （el）非线性积分微分方程组。这些方程是耦合的：耦合表示电子之间的库仑相互作用。因此，由于我们已经从线性微分方程转向非线性积分微分方程组，因此问题相当复杂。非线性破坏了任何积分的可能性。但哈特里惊人的直觉打破了僵局。
　　具体来说，他初将一组测试函数假设为未知函数，这些函数恰好是布洛赫波。这使我们能够确定从非线性项（测试函数的模平方）得出的电势，然后我们继续积分方程组，这些方程组现在不再是积分-微分，而只是微分（薛定谔类型）。如果我们将使用 Bloch 波的近似值称为 0，则新系统的解将近似为 1。
　　对于后者，我们重新计算非线性项（Hartree 势）引起的势，然后再次继续对得到的系统进行积分。这里的解近似为 2。以此类推，该过程被迭代。算法的收敛性在近似 s 的某个阶数处达到0使得获得的结果（特征函数、特征值、Hartree 势能）与 S 阶的结果一致0? 1，在所需精度的范围内。相应的 Hartree 电位称为自相容（或自洽）电位。这就是为什么 Hartree 算法被称为自兼容（或自洽）字段方法的原因。

关键词：金属导电电子

上一篇：IGBT基础入门

下一篇：氧化镓异质结二极管展现了雪崩和浪涌稳健性